How to Beat the Impossible Freecell Game
On Windows, Freecell game #11982 is impossible to beat. But there is a way, albeit unorthodox.
Open up Freecell and hit F3 (or Game -> Select Game) and type in 11982. Hit Control-Shift-F10, then move the 2 of hearts to the 3 of spades and voila, you won the game. At least, that’s what your game statistics will say.
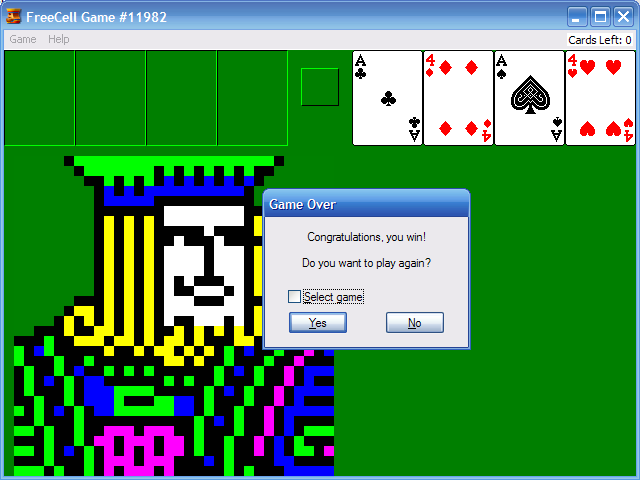
Update: If you think you can beat this game, check again. This is the starting layout.

The FreeCell FAQ declared game 11982 to be impossible after exhaustive research. They wrote, “11982 has now eluded solution by probably thousands of human solvers, and at least eight independent computer programs I am aware of (most of which are designed to search exhaustively for a solution), and I am confident in calling it impossible.”
Re Game No. 11982, which you say is unwinnable. I just played it and won the first time I tried it! Played in the usual way, without the “trick” you described.
Harriet: Are you sure? #11982 has been proven to be unbeatable. You probably mistyped the game number.
Yep, if Harriet comes back with step by step instructions, then I would believe her. I’ve been trying to beat this one for awhile. I haven’t given up hope yet. It always seems like I am one cell short ;)
I’ve won every game from 1 to 11981 and tried for two mo. to win 11982. Don’t believe it’s possible in the conventional way.
#11982 is not PROVEN to be unbeatable (extremely hard to prove something like that), but is BELIEVED to be.
@Frank Correct.
Game is impossible, i tried it. the only way to win is by cheating or glitching
http://freecellgamesolutions.com/ds/?g=1982&p=aiq
@hossi That’s 1982, the impossible game is #11982.
Before realizing the game was impossible, I came across it at random. I can’t give up on a game without winning, so naturally, I played this hand over and over again. Never won. Is this hand still proven to be impossible? I see that one user posted he/she beat it on first try. Really??
@Jennifer No one has ever beaten the game and shown how it was done. I can guarantee Harriet didn’t beat it on the first try. She played another game thinking it was 11982. If you do beat it, you’d immediately become a Freecell legend.
How about help on 25450?
I have completed 16710 games in a row except 11982 keep going back to 11982, findly went on line to see if possable,glad I did after 500+
attempts over 2 years time. thanks people
@ralph That’s true dedication.
The picture above with the 11982 game won is fake.
Try to open the game, than hit ctrl+shift+f10 , hit abort, than move a card and the cheat is done.
I also tried 11982 but no succes,
best regards,
tibanu
@tibanu Did you even read the post?
I play freecell evryday @ work and i beat it with no cheats, it is very easy, i have come across some that were more difficult than that.
@iplayzharder You played a different game. If you don’t believe you did, what was your solution? Wambooli couldn’t solve it and offered a $25 prize for someone else to solve it, but no one could. The FreeCell FAQ declared it to be impossible after exhaustive research. I quote, “11982 has now eluded solution by probably thousands of human solvers, and at least eight independent computer programs I am aware of (most of which are designed to search exhaustively for a solution), and I am confident in calling it impossible.”
If you were able to beat it, how would you ever prove it? Are you expected to remember each move and be able to repeat it?
@Champswest The easiest way would be to record the screen as you play the game.
hi have yall ever tried #-1 that i think is impossible!!!!
I did not know that many people had already written about game no. 11982. I came across this game and was trying for two days, every time hitting the impossible position. Perhaps the reason is that four number sets are piled one on another in this set. They are Black 5, Red 9, Black 4 and Black 7.
I’ve won games 1 thru 21605 to date but never won 11982. Is it still proven unbeatable?
@Sam Yup :)
I doubt that any computer program searches exhaustively; I think that would take far more computational power than anyone has. But it still probably has no solution. What are the odds that there is a solution or class of solutions but only when done by one very precise and unexpected sequence of events? Usually there are a LOT of ways to do them, that’s why it’s so easy to stumble onto one of them.
@fred Most programs search exhaustively and at least eight independent programs were unable to find a solution. A game like FreeCell isn’t all that complex and with Moore’s law we have access to more and more of it. With today’s processors, a hundred million combinations can be tested in seconds.
I have played every game up to 27730 sequentially and the ony one I couldn’t beat was 11982
@Fred Computer’s can be extraordinarily exhaustive at searching. All it takes is for someone with expert level skills at scripting, to create an Algorithm that would explore every possible move, every certain pattern, and every combination in and there of in a single scripting program. Even if there were a million different types of ways to attempt to solve it, a program can run through all of them. Trust me. Hackers do it every day to crack codes, algorithms, passwords.
Impossible FreeCell Game # 11982 other way
http://www.youtube.com/watch?v=QZrnB0BgKA0
We should start a collective fund that is payable should someone be able to beat it legitimately and prove it. $25 isn’t enuf, get it up to like $1000000 and we would get some attention!
@rknell85 That’s a great idea. I would be willing to put up $1,000 for anyone who can beat that game using only legal moves (no tricks).
Just ran freecell 11982 through a computer program designed to beat these type games. After 20,000 attempts and no success, I pulled the plug. I believe the game is unbeatable,the only free cell game I’ve ever found that can;t be beat and I;ve been playing since 2000.
@cattrick Thanks for adding even more evidence to confirm our theory that game 11982 is unbeatable.
I wonder if these programs include moves where you would take from the foundation pile to help complete a black red black red pattern. As far as I know this is a legal move in freecell, albeit a bit unorthodox.
@William As far as I know the programs are extremely thorough and try all possible legal moves.
I won it after a few ‘f7’ undos to the beginning. The first time took me 40 minutes. The second time, ten. How do I get my $1000? LOL.
@Keith That’s fantastic! Just send me the steps to beat the game. They can be written out, a screen recording, using Microsoft’s Problem Steps recorder, or whatever else works. I’ll gladly send you $1,000 (I’m not kidding).
Update: As of 10 Apr 2014 Keith never replied to my request.
Obviously, one can easily place the cards into an unwinable hand; that’s trivial. Since unwinable hands have been proven by example to exist, it seems logical that a pseudo-random deal would, eventually, produce such a hand. If I were designing the game, instead of dealing randomly, I would start from a completed game and make a pseudo-random sequence of legal backward moves to arrive at the starting position. Such an algorithm could not generate an unwinable game. If it were able to generate #11982, then it would be solvable.
At least one would be able to say with certainty that all games generated would be winable.
@Steven Smith (#38) (commenting on my own comment)
I should have thought about that one more deeply. One gains nothing by working backwards… it’s exactly the same complexity. Obviously, I can generate *some* board state by inverse plays. From there, my “deal” algorithm would have to solve the issue of getting all 52 cards onto the board; I’m guessing that this would prove to be equally as difficult as generating a solution in the conventional manner.
I’ve been playing FC for years and have even created a log of hard games. I’m stuck on #1941. Just want to know if anyone has won it. Usually I’ve gotten the solution at most 10 tries. I’m stuck after 10 moves on this one.
@Will Here’s a video of how to beat that one. http://www.youtube.com/watch?v=1J2LOCVQhuI
Thanks Dan I’ll try a little longer before I view the answer. I’ll let you know which way I went.
@Will That’s a tough one. I tried several times, then gave up and looked at the solution.
I guess this is the one of the few I’VE BEEN LOOKING FOR!!!!!!(:-))
Talk to you later.
I’ve just wasted the last two hours trying to beat this Freecell puzzle. I finally decided to search the net and see if anyone else has had as much difficulty with this game as I have… I wish I knew the game was “unwinnable” two hours ago. lol :)
@Nat I know the feeling. I was stuck on the game for quite a while myself :)
If it is possible to beat, there’s a very small chance that someone might solve it not knowing that it was thought to be impossible
I doubt that will happen though
@KoreusZ I don’t deny there’s a minuscule chance, but it’s so small it’s hard to take it seriously.
I’ve been playing Freecell eversince and just encountered this game today. In the pretext that all freecell games are winable, I just couldn’t solve this one. So I went to the Net only to find out that there are lots of guys who find it impossible to solve.
What does Microsoft, or more specifically the original author say on the subject? Did they generate the game sequences by working in reverse? If not, how did the exclude other “unwinnable” combinations and still retained 11982? I am a frecell addict as well, with a win percentage in the 90’s and have hite triple digit win streaks. I remember tangleing with 11982 a couple of years ago, but after the destruction it was doing to my my win percenage, I gave up and forgot about it till just now.
@Birdsong I don’t know of any official comments from Microsoft or from the developers on how they generated the games. Sorry about the damage to your win percentage ;)
The Freecell that came with Windows XP said that “It is believed (though not proven) that all games are winable.” I agreed with that since I’ve never lost one (thousands and thousands played randomly) until I came to the dreaded 11982 a few days ago. I tried for several hours to no avail. Though it can’t be PROVED impossible, the evidence weighs STRONGLY in that direction. No? One more vote for impossible from me.
@Laura That’s interesting about Windows XP saying that. Thanks for the addition.
There have been a few games that I have tried several times and given up on, only to go back to the following day and beat easily. BUT I have been working on 11982 off and on for maybe 10 years and still no luck.
@Carol Thanks for yet another vote that the game is unbeatable.
Thanks all, so glad I thought to look on line – I shall now give up with 11982 – though maybe just one more try :-)
@Anne No harm in trying ;)
play at 100% @1200 games but hit 11982 and wasted several days!
Glad someone said I had not lost my stuff. moving on at at 100% any more
@phil Wow, 1200 games!
with the aces so deeply buried instinct says this would be a very difficult game at best. i shall try it without any hope of winning!
@gor That’s a great attitude. And if you can prove you won, I’ll give you a $1,000.
Thanks for this post. I was stumped by 11982 for the last two days. A few Freecell versions ago (XP, maybe) I remembered reading that “all games are winnable.” I checked the “About Freecell” section of the game a few minutes ago and noticed the message was gone. Thanks for saving me some sanity. …But now I somehow feel the thrill of Freecell is gone. An unwinnable puzzle always makes you feel cheated. *Smiling*
This is not the Microsoft version of freecell but I think I found one that is not beatable and if you can beat it please send me the way you did it my email is jmullins875@gmail.com… here is a link to my screen shot….. http://grab.by/sMxK
I have tried to figure this out for about 2 days now and I have had no luck so I am hoping that someone that is better at freecell will not have any issues solving this!!!
Thank You ALL for saving my sanity!!! Got snowed in for a couple of days and had game 11982 from the first moment I sat down to play. I even told my spouse that I didn’t think this was winnable. Now I can walk away without feeling the exasperating all-consuming need to win this one!!!
@Laura : the problem is that “impossible” is not a political issue, but a mathematical one :-P
What’s interesting me the most is not is this game is possible or not, but the way games are created.
Freecell games are obviously created in a pseudo-random way, they’re two obvious way to create a game :
– the way explained by Steven Smith, which can’t create an impossible game
– The “stupid-one” : put the card in a random way on the board.
The second one can obviously create impossible game, and 11982 might be one of them.
However, it seems it’s the only not-sure-to-be-winnable game, for 32 000 games.
Then we should look at the probability to create an impossible game with the second algorithm.
If it’s about 1/32000 or less, then this algorithm could have been used by Microsoft to create freecell game.
If it’s like 10%…
I don’t know the solution of my question, however I think there are “many” impossible starts which could lead to a lose.
According to me, there are 3 options :
– I’m wrong about the “quantity” of impossible starts, then 11982 could be one of them
– The Steven Smith algorithm is the good one, then 11982 is theorically possible, but could need like 1000000 plays to be win.
– A non-trivial algorithm has been used to create freecell game.
I’ll think about it… ^.^
Btw, sorry for the mistakes I could have done, i’m absolutly not a native speaker ^^
I have been trying for two days to beat 11982. I have a run of 5400+ without a loss. In the end I Googled and found this site. Like so many others, I wish I had looked earlier:). I thought I would be in for a tough time with 11982 when I saw that all four aces were hidden either at the bottom of card stacks,or in the case of the ace of diamonds, one down from the bottom. It makes it nigh on impossible to start clearing the game of cards before they start blocking avenues of play.
I used to gleefully watch my own stats mount up until I found by accident that, when a game becomes obviously lost, you can just restart the PC without closing Freecell and, Hey Presto, the game is forgotten and your stats remain untouched. Now that the stats are less important I find each game is more fun for itself. Before I start I can set myself other tasks to achieve, such as making sure the aces line up in a particular order as I free them, or seeing how few cards other than the aces I need to remove before that final rush of cards to victory, (I have once managed only the 4 aces and a single 2). That can make a relatively simple game take on a more challenging aspect.
Is that just plain too nerdy?
I’ve noticed a lot of comments here over the years saying things along the lines of “this can’t be proven impossible”. This is a mathematical problem, and as such absolutely can be proven impossible. And it has been.
The simplest, and longest, way is simply to try every possible set of moves at every juncture until you reach a point where there are no moves left to make (or only moves that go in a loop, like moving the same card back and forth), and no solution was found. There are numerous freecell solving programs out there that do this (despite some concerns above about processing power, this kind of task is exactly what computers do well and far within the capacity of even an older computer to do quickly) and, as mentioned in the article, many have been applied. So there is no clever solution waiting that simply hasn’t been found, because literally everything has been tried, multiple times.
So let’s be clear; this puzzle isn’t highly improbably, likely impossible, or nigh impossible. It is simply impossible.
@Adrian Without having seen or run the programs used, I can’t say with 100% certainty that it’s impossible, but you’re probably right. However, I’ve never seen incontrovertible proof of your claim. The chances of a solution eluding millions of attempts is certainly low, but I would like to see a mathematical proof that the starting configuration of #11982 makes winning the game impossible.
@Dan In that case, surely you can easily resolve this by running some of those programs yourself and seeing what happens? The Freecell FAQ linked above mentions several I believe. Otherwise, arguing that “we don’t know it’s impossible because maybe every human and program has made a fundamental error that would otherwise to make it solvable” sounds about as useful as “we don’t know that 2+2=4 because maybe every person and calculator has been making the same error”, without ever actually examining a calculator. It can be considered possible only by dismissing a truly staggering amount of evidence to the contrary.
I’m half tempted to write my own brute-force solver and put up the results and source code for you.
I get what you’re saying, but basic math and Freecell gameplay simulation aren’t equivalent. Really, we’re splitting hairs here. I’m just saying there’s a minuscule chance someone missed something, and you’re saying there’s no possible chance of error.
on the question of 11982 if you shuffle a pack of cards you are doing it in such a way that no person living or dead has ever done before or will ever do so in the future taking this in to account would it not be foolish to conclude that there are no more 11982s lurking out there
@Dan But that doesn’t make sense in a limited domain like this. There are an absolute number of possible… you know what? That’s it. My task for tonight (well, OK, might take a few days); write a brute-force Freecell solver, with source (because I guess you need to see the innards to be super certain,) to demonstrate, definitively, that there is no, no, NO solution to this puzzle. Stay tuned.
I don’t feel the difference between “possible” and “impossible” is “splitting hairs”, I think it’s a fundamental issue in the discussion. With that in mind, and because I’m a money-where-my-mouth-is kind of guy: https://drive.google.com/folderview?id=0B1j_Jk2qDT_4QnVRWkRrcGdrU0U&usp=sharing
Welcome to cell11982, a brute force freecell solver, by default set up to test the impossible puzzle, 11982. Three files are at that link. cell11982.py is the python program. Python programs are compiled on-the-fly, which means the program is the source code; you can open it in any text editor and see exactly what the program is doing. Source Explanation is a more detailed explanation of what the program is, how it works, and what it means.
11982 results.txt is the (rather large) results file. You will probably want to click the download link in the bottom-right corner and view it on your computer, rather than wait for Google’s preview of all 36+ mb to load up. This lists, literally, every possible layout of cards you can reach for 11982, and (if you wish) can trace them back to see what moves were made to get there.
It doesn’t even get close.
There are paths that lead to two hearts being sent home, or two diamonds… but these are exclusive. Getting the ace of one puts you in a position where you cannot reach the ace of the other. Clubs and spades? Forget it; you can’t even get started.
But don’t take my word for it. Check the layout I’m using, peruse the code, run it yourself, browse the results. Set up some solvable puzzles and see if it gets there, or put in obviously impossible ones and see if it throws them out. If something’s been missed, then good news; you only have to check a few hundred lines of code (included comments explaining what’s going on) to find it rather than well over 80,000 individual board layouts, a relatively simple task.
For this puzzle to be possible, either I’m not correctly testing for every move that can be made on a layout, incorrectly discarded valid moves, or not sending every valid layout to be tested. If I’m not doing any of those things with this program… and anyone can see for themselves whether I am… then all possible minuscule avenues have been covered, and the puzzle is impossible.
@Adrian Nicely done. I am really and truly impressed you did this.
You’ll probably think I’m just being stubborn, but I maintain that you have only proven your program can’t solve the game, not that the game itself is unsolvable. You haven’t proven you’re correctly testing for every move, or not incorrectly discarding valid moves, or that you’re not testing every valid layout to be tested. You claim you didn’t omit anything as a fact, then ask others to prove you wrong.
In your comment, you were approaching the kind of proof I was looking for by discussing a step that needs to be reached in order to win (like getting the Ace of clubs or spades out), then showing how achieving that is impossible (easier said than done), which could then be used to prove the game is impossible. But I have yet to see such a proof.
Writing a brute force program is useful, but as a fellow developer, we both know bugs can easily sneak past watchful eyes. (e.g. Heartbleed…). Can you prove your program (or any of the other solvers) don’t have a bug?
Using Proof by Exhaustion is probably the best approach for proving this Freecell game impossible, but even mathematical proofs have been later proven incorrect.
After trying yours, I downloaded a few more solvers – FreeCell Pro, Don Woods’ c program, FreecellJSolver and this online version. Of course they all found 11982 to be impossible.
And as a side note, for anyone who thinks they can solve 11982, download FreeCell Pro and play the game so it will log your moves.
@Dan But, again, it’s a limited domain puzzle, so we the statement “you have only proven that your program can’t solve the puzzle” doesn’t make sense. Either it can solve Freecell, or it can’t. We know that no legitimate Freecell solution is going to involve moving two cards at once, or having a 5th freecell, or a 9th column, or starting a home cell at King and working our way down. It’s not like heads or tails, where someone may cry “what about the edge?”. In Freecell, nothing is hidden. We know exactly what’s possible, and if we’re testing for that, then we have our answer.
Bugs can sneak past but, as a developer, you know we can test by example. Oh, sure, if a bizarre input comes into play maybe some weirdness will occur, I daresay you can trip my program up by substituting cards with strings of random characters, but that’s not relevant to this discussion: we have one set, simple layout, and that’s what we’re testing. We don’t have to worry about complicated maths or string handling messing things up, because it’s not here. We know it doesn’t crash out part way because… well, firstly, because I’ve run it fully, and second, because you can too, so it definitely runs well enough to reach the end. The example test board included in the source (an almost complete board) takes less than a second to run, useful to double-check if the program will run to completion (without exhaustively testing each element on the way). As such, we can see that, at least, the system as a whole works correctly sometimes. We’re now into unit testing, seeing if each part of the machine acts the way it should.
If my program (or any program) can be demonstrated to make each individual type of move possible, for example, then we can cross this off the list; there isn’t a bug causing particular kinds of moves to not be made. It’s possible that, for example, an off-by-one error could mean the system was ignoring the last column, but we can easily identify that. I know that because at an early stage, the program *did* have that same error, and I did catch it. In the results we can see cards are moving to and from every column and freecell area. So that’s one factor we can tick off, we know it’s not ignoring any position. The same way, we know it’s moving to and from the top card of each column, that it can take the bottom card of a column and repopulate an empty one, that it’s making use of all 4 freecells and that it can, at least with hearts and diamonds, move cards home.
“Ahhh”, I can hear you thinking, “but what if it can’t move ALL cards home? Maybe it’s stopping at 3?” And I fall back to the same reasoning; if the input is valid, the process isn’t falling apart at the extremities, we can see it’s working in some places, and we can’t see any place that it’s wrong, then it’s right. In this case, we can look at card list in the source and see if there are cards missing, or in the wrong order, or check for indexing errors. But that’s all; once that’s all there, we can tick this off, it works.
Perhaps it’s missing layouts? Afraid not. The way the program works means the list of boards is initially populated by just one; the starting board. Generally, we’d expect an error resulting in the first or last element of the array being skipped or going past the end of the list. But here we know it isn’t going past the end of the list (because otherwise it would crash out every time you ran it), and we know it isn’t skipping the first/last element because, at the very start, it only has one; skipping this would mean the program would never run. And we know it isn’t skipping out on saving elements along the way from way back in that first bug; we can see it saving every move in the results, and we can see moves being made from each layout thanks to the “parent layout” tracker (a late addition in development, but I’m glad it’s there). This is one of the easiest things to check, in fact; just see what moves can be made from the initial layout, and these will be the first set of moves in the results. (You can do the same check at any point, but bear in mind some possible moves may have resulted in a duplicate layout of an earlier one and so be shown earlier, with a different parent).
Remember: when we’re saying “maybe there’s a bug”, we aren’t just suggesting a bug is there in my program, but that *every single freecell automated solver and human player, ever, has been making the same error, on just this puzzle* (amongst the first… 10,000? Is that correct? I know later version of MS Freecell had higher numbers of puzzles with more unsolvable ones). Likewise, when I say “you can see for yourself”, this wasn’t me saying that it might have bug and I wanted someone else to test it… it was me saying I *had* looked for bugs, weeded them out, but that I don’t expect my word to be good enough.
But I’m going to go one further here. My email address is right there in the source. So if you still feel the burden of proof is on my end (and I’d argue I’ve submitted plenty at this point), then tell me what tests you’d need to be certain. Do you want a running tally of how often cards are moved from each area, to eliminate the possibility something is being missed? Perhaps you’d like it to track how often each card is moved along with how often each card is on the bottom of a column, to identify if cards are being revealed but never moved? Or maybe you just want full test boards, to prove that it can move every card, and is checking everywhere? Whatever it is, and this is an open invitation, my email is right there. Tell me what proof you need.
For now though, I am confident in saying once more; this puzzle is impossible.
Man oh man that’s a comment and a half! :)
My point isn’t about bugs in your program. I didn’t find any bugs either, or in the other solvers. But even if we had a billion other solvers all declaring the game impossible, a valid solution would prove them all wrong.
Albert Einstein said, “We can not solve our problems with the same level of thinking that created them.”
In other words, if our knowledge of FreeCell isn’t as advanced as we thought, and we missed something, then a solution that we had never considered could be found.
My argument can be summed up thusly.
Not being able to find a solution is not proof a solution doesn’t exist.
However, with that being said, I concede FreeCell falls within the bounds of an NP-Complete problem and can therefore be computationally solved with brute force analysis as you have done.
In short, I too am confident that game 11982 is impossible.
So far, I’m at 3,000 straight wins without a loss. I really don’t look at the game # so I couldn’t even say if I’ve ever come across game #11982. Will look for it from now on.
I have Windows 8.1 and found another one I believe to be unbeatable: #6362856.
@WillH Assuming this is the same game you’re referring to, my FreeCell solver says it’s winnable.
I have 4651 wins and 0 losses. came across game 11982 and as always, before I make a move I mentally drill each stack down to the bottom. It didn’t take long before I realized 11982 was going to be a tough one. Now I realize probably impossible. I discovered this forum and it confirmed my belief. My little game is to not use a free cell to win a game. Of my wins I was able to win 62 games (Being a baseball fan, I call them perfect games) that way. And yes, I do have a girlfriend,, play a shitload of golf and have a decent tan.
Thanks to Dan, and to Adrian for his computer-generated proof of the insolvability of 11982 using the method of exhaustion. Freecell is much simpler than chess, which is not solvable in such a way (or any way, for that matter). I have a long list of freecell games that I found “difficult”. For me, 17993 had been the most recalcitrant. However, after about 50 tries at 11982, I consulted the Internet. Thank goodness! One shorthand of the play of the game would be to give the origin and destination of each card. So moving a card from col 1 to the holding zone might be written 10, or moving a card from col 7 to its appropriate suit 79. So a game might begin 59 18 82 and so on. This is clearly a unique and complete way of writing the game. Incomplete but suggestive would be simply to use the column of origin: the same game would start 518 in this notation. Might use 0 for promoting from the holding zone. This latter method would be more in the nature of a hint than of a replay.
“Clearly” is a kiss of death. A unique notation would differentiate the four places in the holding area, say as a, b, c, d. Sorry for the slip.
I thought I could beat them all. Not this one. It’s nice to know that somebody else couldn’t beat #11982.
I use the android freecell game (on my phone) from http://www.odesys.com and have played every game consecutively starting at game 1 and have won all 11981 games (using undo as needed)…until I hit 11982. Usually, if it takes more than 30 minutes (like one in a thousand games), I look up a solution online. I could see “by inspection” that 11982 was “probably impossible” because of the location of the aces and the stacks above them, and after trying to solve it for about 30 Minutes.
Your posts here have been very helpful in convincing me to go ahead and ruin my 11981-game winning streak . I don’t think there is any way to restart my phone or shift-f10 or anything similar to work around this issue for this android version of FC, but if anyone out there knows of a way to avoid ruining my 11981-game winning streak, please let me know. I guess I can just “start over” consecutively again at game 1 and remember to skip 11982 when I get to it next time.
I hope I remember to skip over 11982 next time. I will stop playing for a few days in case a work around gets suggested here.
Thank you everyone for your dedication!
@albie I am also a nerd. I managed only two aces and one two.
With no suggestions on how to prevent ruining my 11981 winning streak (playing consecutively numbered games starting with number 1), I will just reset my game statistics and “start over” with game number one, and plan on remembering to skip game number 11982 after I win the first 11981 games again. That should only take a few months or so. Again, I appreciate everyone’s dedication to the game.
I cannot beat #1941
Here’s a video of the solution: https://www.youtube.com/watch?v=1J2LOCVQhuI
And the steps to beat it. Numbers = column number, letters = 4 free cells (a-d) and h = the home cell.
42 87 1d 1c 15 c5 3c 3b 3a 2h
5h 15 16 37 83 81 c1 7c 73 c3
7c 7h 71 73 71 21 23 87 5h 53
52 32 38 28 23 83 82 58 5h 2h
1h 68 67 17 81 28 c2 1c 71 c7
2c 26 c2 26 24 3c 38 64 c8 5c
52 65 45 46 56 54 a5 64 6a 65
a5 2a 26 45 42 52 54 24 25 45
42 52 54 a6 24 25 1a 12 a2 1a
16 45 41 51 54 a6 14 15 45 4a
41 a1 2a 26 51 52 12 15 a6 25
21 3a 32 35 31 51 53 21 a1 6a
62 a2 7a 76 26 27 12 67 6h 1h
13 15 35 31 51 53 13 15 35 31
63 6h 51 5h 4h 41 21 72 73 23
72 76 26 37 a3 4a 32 36 76 87
81 71 b7 6b 26 d2 3d 63 b6 2b
a2 6a 36 b3 8b 68 a6 2a d2 6d
62 d2 6d 64 d4 2d 24 d4 2d b2
1b 12 b2 4b 84 d8 4d 48 b8 3b
83 d8 7d a7 1a 17 a7 1a 15 a5
1a 1h dh 6d 61 d1 6d 38 23 27
2h 7h 62
Have been playing for years but just now finding this site. Enjoyed reading all the comments esp regarding the elusive 11982. I mean the impossible 11982
Okay, I’m not at the skill level or competence of you guys, but I’ve been stuck on 6911962 and just can’t see any way of completing it. Can anyone give me a heads up on how to do it?
Many thanks!
Here’s a solution from the FreeCell solver:
Numbers = column number, letters = 4 free cells (a-d) and h = the home cell.
3h 54 48 4d 3c c3 4c 46 3b 36
64 6a b4 35 6b 63 b3 a3 5b 65
67 63 43 4a 68 36 34 a3 63 2a
26 34 a6 2a 21 c1 51 b5 2c 8h
23 4b 42 b2 4b c4 1c 51 c5 2c
32 c3 6c d6 86 8d 84 82 82 8h
dh 1h 51 5d 51 b4 87 57 5h 5h
4b 48 45 85 b5 4b 41 c1 7c 78
74 84 c4 1c 18 c8 2c 23 c3 2c
25 c5 1c 12 c2 1c 14 c4 2c 24
c4 1c 12 17 a1 71 7a 4h 3h 71
c1 71 d1 41 4d 4c dh ch 73 1h
1d 14 1c 17 18 16 12 a1 81 71
c1 41 4c 4a 46 d1 a6 c6 3d 35
3h 5h 6h 3h 1c 1a 16 18 17 12
14
Thanks Dan! Very happy now I’ll be able to do it :)
Have a great day,
Shaz
I came to this page defeated, but at least I have company.
“It is believed (though not proven) that every game is winnable.” -Jim Horne
That sentence….that (damned) sentence….
I feel your pain, but at least you know now :)
i am very dissappointed because 11982 is impossible
This game is solvable if there are 5 free cells.
61 54 78 1e 1d 61 5c 51 1b 51 51 4a 54 d5 e5 1e 1d b1 e1 4e a4 1b 1a d1 b1 5d 5b c5 4c e4 5e b5 6b d5 6d 61 61 46 c4 8c 81 c1 82 e2 1e 71 1c e1 4e 64 a6 4a e4 6e b6 7b 76 e7 28 2e 26 e6 1e 1a 12 a2 e2 5e 5a 15 17 86 57 d5 1d 15 d5 7d 75 d5 7d 71 d1 2d 27 25 75 d5 2d 27 52 c5 7c a7 e7 2e 2a 28 c2 6c 86 c8 2c 25 c5 1c 12 c2 1c a1 e1 4e 4a ah 34 4a 43 a3 4a 42 d2 4d c4 5c 51 5h c1 5c 52 c2 6c 63 83 86 36 c3 e8 1e 1c 12 c2 e2 1e 15 e5 17 1e 1h dh 5h 6h 36 3d 3c 31 37 c1 d1 61 6d 6c 67 31 3h 43 c7 d7 4d 1h 5h 7h a8 2c 25 2h 2h 7h 2h 6h 3h 5h 3a 7h 7h 8h eh bh 8e
Most interesting!
It can be PROVED that not all games are winnable.
Simply choose “Select Game” and enter -1 or -2 (minus 1 or minus 2). Both of those options will deal hands which CAN NOT be beaten. As both of those deals are as probable as as other single random deal of the 52 cards, then that is proof positive that there are AT LEAST TWO hands which simply can not be played to winning.
Perhaps there might be thousands of un-winnable hands ?
TYPO!
as as should be as any
sorry !
As both of those deals are as probable as any other single random deal
I couldn’t help myself doing this – I had to find out.
I wanted to know how many ways it is possible to deal the 52 cards into a Freecell layout. The answer is “lots and lots” !
Wikipedia says:
There are 52! (i.e., 52 factorial), or approximately 8×1067, distinct deals. However, some games are effectively identical to others because suits assigned to cards are arbitrary or columns can be swapped. After taking these factors into account, there are approximately 1.75×10^64 distinct games.
I think that is quite a few, like
17,500,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 different possible starting layouts
It would take a while to play them all.
Charles
As like others, i too have solved all up to 11,981 before been stuck for 2 weeks on the infamous 11,982 before going to the net to find out it is unsolveable. thanks wiki ,i can finally move on to 145,— the next unsolveable one.
@fred 146,692 next unsolveable,looking foreward to getting there!:)
Just did 11982 on third attempt and I’m far from an expert and know no tricks. Took 3 mins +
That’s great – record the screen while you’re doing it using https://www.screenr.com/ and I’ll pay you $1,000.
“It would take a while to play them all.”
At 4 minutes a game average, including “comfort breaks etc”, working 12 hours a day, 6 days a week, 50 weeks a year, a player should manage 54,000 games a year. It would take billions of billions of billions of years, probably longer than the universe will last. I don’t think I am going to start on the task. I have other things to do – like wash the car? Hmmmm … maybe not today – I need time for another few Freecells!
PS – I really REALLY want to see the solution to 11,982. I will put up $500 to the bounty.
Charles
Dan,
I hope you’re right about 11,982 being unsolvable.
I’m in no rush to give away my $500.
Charles
I got stuck on 11982 five days ago, after solving 521 random games in a row. In years past, I’d just move on, but this time around, I am (was) going for a serious win streak. Finally googled 11982 this morning and got my suspicions confirmed. Welcome to the club I guess.
Has anyone considered creating other unbeatable free cell games by starting with the layout for 11982 and then switching any 2 random cards before starting the game? No one seems to have discussed this possibility. Hard to believe that all such switches of just 2 cards would all result in solveable games.
I’ve beaten 11982, but unfortunately there’s not enough space in this comment box to write down my solut
Sure there is! Write it somewhere else, then paste it in. You can add as much content as you want. Or, email me your solution to me by changing the first dot in the domain to an @. I’ll pay you $1,000 if you have a valid solution. But plenty of people have said they solved it, but not a single one of them has ever had any proof. As the saying goes, talk is cheap.
Another one that might be impossible to solve: 9827028. For me the first unsolvable one after 2115 games.
Proving by brute force might be practically impossible – not enough time of living. But I wonder, would’nt it be possible to fomulate conditions that makes a solution (im)possible?
Really? An active Freecell forum in this day and age? Why? Freecell has been a dead issue for a while. Someone on here said he’s got 3000 consecutive wins, and with the current version, you can do that. That sucks.
Another fellow said he had a few strings of 3 digit win streaks and played in the 90% range. Ahhh! A REAL FreeCell player. Congrats! I, too, was a 90%er, and my high streak was 111 games.
I originally played FreeCell in Win 3.1 as part of the MS Entertainment Pack, but started playing seriously in Win 95. At that time, there were 33,000 games available, and I, too, ran across the “It is assumed all games winnable” statement. So, loving a challenge, I set out to try.
And last year I achieved that. Starting at game 1 and keeping track of where I was thru innumerable computer and OS changes, I’ve beaten every game of the original 33,000 layouts, (except 11982, of course. It’s unbeatable, people. Get over it.)
I was originally bummed, however, when I upgraded to Win XP and found that the 33,000 layouts had become a million! So in 2003, the achievable goal I had been working towards for 8 years became unattainable, but at least FreeCell was still FreeCell. You could back up one move, and that was that. When the “There are no more legal moves” screen popped up, it was game over, and one loss attributed to your stats. If you closed the game, you logged a loss. If you replayed the game, it was a loss, but you could replay until you won for only that one loss.
Bottom line, stats, percentage of 1st time wins and win streaks were challenging. It was the chess game of solitaire. You had to look seven and ten moves ahead to keep from losing a game.
But a few months ago MS forced me off of XP and into Win 7? And I was disgusted. You can play till the “No moves” screen pops up, and just back all the way up to the beginning without recording a single loss. 3000 consecutive wins? So what? Meaningless. Had todays version of FreeCell been the one I started playing in 1995, I could have had 33,000 consecutive wins.
But I wouldn’t have. Because 3000 or 33,000 means nothing on the current versions of the game. Microsoft has killed the challenge of FreeCell.
And before it’s said, yes I know there have been independent versions of the game out there that allowed you to back up or restart for eons now, but they weren’t the game that everyone played and everyone talked about. They weren’t the versions that the FreeCell Project was all about. Microsoft’s was. And now it’s dead.
RIP, FreeCell.
I have been playing Free Cell No. 11982 for a few hours now and I am finding it impossible and frustrating – YES frustrating. I have been playing the game Free Cell now for a few months and have WON almost 179 games in a row. I actually played 234 and it shows 1 loss… but actually my computer shut down so that shows as a loss.. So really that shouldn’t count. I just checked on the net to see if there was something special I could do. So I just happened to land on this site and low and behold it shows this game. I thought maybe I was losing great streak or losing my mind (LOL). So I will keep reading on this site and see if there is something I can do. Does anyone have any great ideas or do I just let it go.
Another thing, being it is late at night, can I somehow save this game and close my laptop down for the night without losing the game. Or should I just give up and turn it off.
Thank you,
Ooops… Error in sentence structure: ABOVE
I thought maybe I was just on a losing streak or losing my mind (LOL). So I will keep reading on this site and see if there is something I can do. Does anyone have any great ideas or do I just let it go.
HOW TO RECALL EACH PLAY IF YOU WIN
I just remembered how one could recall each play… If you win the game, you can write the plays down by doing it backwards. You do this AFTER WINNING… start by clicking “Control Z†that will take you back one play, write that play down. Keep doing this and write down the play each time.
After that write each play from the end to the beginning and that will give the correct plays to win the game.
GOOD LUCK … If anyone gets it please let us know.
Guys, I’ve been playing Free Cell game for the last 12 years.
Game #11982 has been proven to be unbeatable, get over it !
I have solved game # 11982 , but I can’t show you because there will be a price for anyone who has solved it.
sorry
Dan,
Why didn’t you post my comment dated 2/24/2015 ??
It works perfectly in Windows XP, but Windows 7 fails to use the cheating method
Why do you need to cheat in the first place?
has anyone solved #5926934 on win 8.1? so far it has eluded me after 2hours+.
Game #5926934’s Solution using 4 free cells.
1a 1b 81 87 a8 78 3a 3c 32 13
43 42 1d 18 c1 21 2c 25 b5 6b
65 d6 2d 26 b6 2b 21 3h 4h 72
78 b2 35 a3 62 52 81 c7 87 6a
65 63 53 87 47 57 38 4h 36
After wasting at least an hour on 11982, my online search for a solution lead me here. Thanks for letting me know 11982 is unsolvable. After bailing out of that game, I was dealt 16351 by my computer. This was a sweet follow up game, because I was able to play it down to two cards left; the King of Diamonds on top of the Queen of Diamonds.
is there a game that can be won with all the cards being stacked before the first ace moves to the top
1941 I had no issues with – 3 attempts… roughly 30 minutes. I’m working on a list of ‘hard’ freecell games and happened across this site. Never realised there were so many other affecionados of this humble game :0) FYI, i’m on the XP version.
I’ve played this game for years as part of my daily routine. I always play one game before starting work, plus the odd ones through the day. Managed 750ish win streak and I’m on 99% win percentage.
Impossible game? I’m sure as anyone that it is.. but maybe.. juuuuust maybe.
Knowing my luck, I’ll solve it and due to never recording moves (or much else in my life to be fair!) I’ll never be able to prove it!
Cannot find the Freecell game with options to select game #.
On Windows 7, it’s Game > Select Game, or F3.
Cannot find the Freecell game with option to select game # in Win 8. Can the original freecell be downloaded from somewhere?
I don’t know about the Windows 8 version, I haven’t used it. But if you happen to have access to Windows XP, you can run that version on Windows 8 by copying over FreeCell.exe and Cards.dll in C:\Windows\System32.
Thanks for the XP FreeCell version. I do have an XP installation disk but don’t know how to copy and then install that Freecell into Win8. Any suggestions? Thank you for your come backs.
I’m not sure. I think the installer disks store the files in CAB files, so you would have to find the CAB file, extract it and copy the files over.
Thanks for you help and suggestions. I might try it. I”ll think about it, Jay
i even went with the only logical way to play is to play illogically …. and lost.
I feel bad for the guy who set out to re-play 11981 games to reset his stats. I’m surprised all the techies on here have not mentioned the Windows Registry. Freecell stats can be manipulated there to whatever ones wishes, including removing losses. If you are into cheating, that works.
I bet some of the solvers above did a re-start trick on old Windows as I saw a solution on YouTube where if the game was restarted followed by an Undo, the 8D moved over to column 8 and then the puzzle becomes solvable. There is no restart/do-over in Win 7 – but you can Cntl-Z undo multiple moves all the way back to the beginning, unlike the older Win XP version. My XP machine does that trick – restart 11982, do an UNDO right away and the 8D moves to column 8 and the puzzle is solvable from there. That doesn’t count.
I agree that with UNDO back to the start, it’s possible to never have a loss recorded, but that should be a loss.
I had played 5,650 games over the years with no losses until yesterday; although I had not idea how to prove it, or even if such a proof is possible, I had suspected that the game is mathematically winnable. However, yesterday I came upon game 131,990,624, which I have not yet been able to solve. I then asked “Is free cell winnable” in a search engine, and was led to this site, where I learned about 11,982. (I have always used Macs, and it appears that the numbering of games is the same in Macs as in other platforms.)
Frankly, I’m getting burned out on this obsessive Freecell kick, so I will not try too hard to solve 11,982 and take it as empirically strongly suggestive that the game is not mathematically winnable (but it does not constitute mathematical proof because somebody just might back up on a bicycle and solve it without cheating.)
But how about 131,990,624? Is this like 11,982?
Hi Chuck, thanks for the comment. I just ran game 131,990,624 through a FreeCell solver and it found a solution. So now you know it’s solvable. If you want to see the solution, this online solver can show you the way ;).
Thanks, Dan. Now it’s down to 11,982.
Must we wait as long as we did for Fermat’s theorem to know whether or not the game’s mathematically winnable?
I certainly hope not. Perhaps Andrew Wiles could comment…
If you randomly dealt the cards (as you would if you have a flesh and blood deck of cards in your hand), what is the likelihood that the game you dealt would be unwinnable? I don’t really think there is a knowable answer to that question, but if you were writing a free cell program you would need to make sure all your games are winnable. Seems to me that a random deal could produce 20-30% of games that are unwinnable and that freecell would be a pretty frustrating game if not for the programmer not screening out all those unwinnable scenarios for us.
Another interesting question would be if you had three free cells, what percent of games would be unwinnable? what about five, what about one?
1941 is a really tough one to beat. Have not yet got it.
I spent every lunchtime for 6 months trying to beat 11982 and I e-mailed all my free cell pals and no-one has ever completed it. It can’t be done without cheating.
Definitely it’s solvable. I solve nearly 20000 games in a row, was started from number 1 and came close to 20000 but then I changed pc with windows 8 and couldn’t continue. I never give up of solving any game, the most difficult for me was 617, but all others was solved with much less effort (tries) than 617. Now I’m playing on my phone and until now all solved. Just now when I want to download FreeCell on my pc (Windows 10), I accidentally stumble on this discussion and actually laughing on comments that is not solvable. It is, definitely it is!!! Without cheating, without tricks of any kind.
@Leos There’s $1,000 in it for you if you can prove it.
I’ve played and won every game from 1-22934, and so far the only one I haven’t won yet is 22864. There have been others that gave me grief, but I just made a note of it (I keep a running log of the games numbers I play), leave it lay for a few weeks, and usually I go back and can win after a rest from it. My goal was to win all before I die.
Will someone please send me the website to download this version of free cell. patj00@att.net
Dan,
Remember I have offered an additional $500 to add to your $1,000.
So there’s $1,500 available!
So the race is on! Who will claim the money, Leos or JJ Whorley?
Come on guys – Dan and I have put our money up – take it.
Charles
It may be worth considering just what Microsoft means when it says that “It is believed (though not proven) that all games are winable.â€
Does Microsoft mean every possible game? Or does it mean only the games dealt under their programs, which is quite a different matter?
It is entirely possible that they have decided to deal ONLY games that can be won – but they slipped in 11982 by accident or design.
It would not be difficult to arrange the “deal” algorithm so that each game would be winnable – except that damned 11982 of course
Personal Log 1202016:
I too have succumbed to the time sinking activity called Free Cell mainly because Chess Titans turns me into a raging Klingon. So what to do about 11982? Though I haven’t attempted it yet it weights heavy on my mind not to mention I don’t want to lose my 167 consecutive wins statistic. I am considering giving my fellow nerds hope regarding a strategy to defeat the 11982 simulation. I’m going to tell them that its not going to be easy. I will tell them of one man in the future who faced a similar situation. His name, James Tiberius, and while the details of the details are sketchy he managed to re-arrange the parameters of a simulation, in his time, that was impossible to solve and by Grabthar’s hammer, he solved it! The simulation not unlike the Free Cell Conundrum #11982 we currently face was called Kobyashi Maru. Now possibly, just possibly if we meld our collective wits together we too can redefine the parameters of FCC#11982. I think it’s called hacking the program and may require some programming skills and possibly jail time. Nonetheless, I will say to them: those of us who accept this quest and lives to see its completion will forever stand tip toe in the annals of nerd-dom when the Free Cell #11982 Conundrum is mentioned…
God Speed
End of Log
@Xanther May the wind be at your back on this noble quest. ;)
IVE PLAYED 31,500 fREECELL GAMES 5OR6 GAMES I COULD NOT GET. HAS TAKEN ME 15years AM GOING FOR 32,000.wHO HAS A BETTER RECORD THAN THIS?
Hi Free Cellers
FYI, i am not the keith that claimed he solved this one….. as most people on here freecell started for me as a lunch break get away… and before i knew it.. damn i was hooked.. been playing for about a month now, my streak is 300 games… i decided to wiki search free cell and low and behold i ended up here. not believing the gazillion posts i read i decided to check out #11982 for myself, (knowing my streak will be spoilt). why in the name of all things did i do that.. i have no idea…. i then decided to get myself a deck of cards lay them out as per the layout of the game, thought i might get a better perspective not staring at the cards. yesterday i stared at those cards for 8 solid hours… (eating a bag of chips, 2 chocolates and about 3 energy drinks…) this game is something else. @dan, i noticed you posted a cash prize to the winner, i can tell you even if they made it $100000 there would be no takers. i have looked at every possible scenario, if i worked it out correctly if you could get the Ace of spades out you should solve the game. has anyone contacted microsoft regarding this game? Could they have a solution? of the thousands of threads i have read, i doubt it very much…
i never give up on a game, but this one… i will gracefully walk away from. however it would have been super interesting should microsoft actually have a solution and do offer some sort of incentive. put a challenge out there..
cheers to all who tried and lost…
Well said Keith!
As I see it, there is a general assumption “that all games are winnable”, as Microsoft says in the Help that comes with the game.
But, let’s play “Devil’s Advocate” now. What is Microsoft REALLY saying? There are two possibilities, and these are miles apart in their effect.
Are they saying every possible DEAL is winnable? That cannot be true because it is immediately possible to deal layouts that definitely can NOT be played to win – just select games Minus 1 or minus 2 (-1 or -2) which are impossible, obviously so. Have a lok at my post of 28 November 2014. There might be any number of other “impossible” deals.
I think that when Microsoft are saying “it is believed but not proved that all ganes are winnable”, that they refer ONLY to the deals offered in the games, and I believe that WITH ONE EXCEPTION, 11982, that may well be true. I believe the algorythms that deal out the games do so from a “won situation”, as if randomly dealing the cards back from four completed home stacks.
This begs the question about 11982 – did Microsoft accidentally include an impossible game (which I feel is unlikely considering how the program probably works), or did they do it deliberately to stir up some interest and controversy? If the latter, they certainly succeeded. I feen Dan’s $1,000 and my $500 are safe enough!
My grandmother(I am 17), has played this game, starting from level 1 to level 33k and something, for 5 or 6 years now. Recently I heard about the impossible level, and I thought that she hasn’t reached it yet. Today I asked her if she has beaten it, and she told me that she has. I didn’t believe, but she has several notebooks where she writes all the levels she has completed, I checked them, and indeed she has written 11982 there. What if she really has completed it?
As a reminder, this is what they say in the XP version:
“It is believed (although not proven) that every game is winnable.”
Does that mean every possible deal, or does it mean only the games offered by the program? That’s THE question.
When contemplating this enigma, consider games -1 and -2.
Oh yes, and let’s not forget 11982 either.
Charles
Have her try again while recording her screen with something like Problem Steps Recorder. If she does it, I will pay her $1,000.
Nexson,
You ask “. . . she has written 11982 there. What if she really has completed it?”
Well, as Dan has told you, you and Grandmama will win $1,500.
It’s that simple.
Bear in mind that even though Microsoft says “it is believed but not proved that all games are winnableâ€, it can be proved beyond any doubt that it is NOT true that ‘all games are winnable’. Just select game -1 or -2, and those games will be dealt up, and they are NOT POSSIBLE to solve, obviously so, even though both of those deals are still the full 52 card deck. It is clear that it is possible to deal other games which CAN NOT BE SOLVED without cheating, but these are not so obviously unsolvable as -1 and -2.
Game 11982 is one of those unsolvable games, probably one of thousands or millions or trillions of unsolvable games.
Break the new gently to Grandmama!
Charles
This is pretty strange but I was having an issue with another Freecell game and came to google to search if anyone else had a problem with it – then came across this page. I saw the game listed here as impossible to beat so I thought I’d try to play it as I’d only come across one before that I couldn’t crack eventually. I went to this site – https://cardgames.io/freecell/ and selected to play game 11982 and started in – within about 10 mins I had a win??? Is it possible this site doesn’t serve up the correct games by number? I’ve done a screen grab of my end frame if you want to see it but doesn’t appear I can paste it here. Let me know what you find out if you can please?
Hi again, will answer my own question here. I decided to go back to the game and restart it – then compare the opening page with your screen cap above – not the same game. I’d already posted on the guys FB page asking if his on-line game followed same number version as Microsoft but have not received a reply yet. Anyway, no need to answer my above post obviously and if I can find an on-line game version that does get me to the actual 11982 I’ll enjoy having a go at it. Cheers.
Footnote to the above – I got a reply from the gent I posted to on his FB page and he confirmed that he did not follow the MS numbering of games. He did say, however, that the only game he has on his site that is unbeatable is #23775. Interestingly, it is not the same game as #11982 so I’m wondering if there are two games in fact that are not possible to win? I have played this game for several minutes and so far have not found a way through but will need to spend more time on it to be sure.
@Reg There are plenty of unwinnable games. You can easily create one if you bury essential cards deeply. But Microsoft said they believed all of their games to be winnable, which makes #11982 interesting.
Hi Reg,
We have all been down the same route that you have tried.
Dan says “Microsoft said they believed all of their games to be winnable, which makes #11982 interesting”. The important word is “THEIR” games, which is definitely not the same as ALL games.
If you look back to my Comment of 11 February ’16, you’ll see what I said then.
Look back to the Comments in November ’14 too.
As far as I know, no authority in this matter claims that EVERY possible deal of 52 cards in Freecell is winnable. I feel sure that is because they all KNOW that not all games are winnable, and very far from it.
It is inevitable that you (and everyone else) MUST agree that “NOT ALL FREECELL GAMES ARE WINNABLE”. Dan and I and many others are firmly of the opinion that 11982 is not winnable.
The instant proof that not all games are winnable is to select games # -1 and # -2. These are IMPOSSIBLE at a glance, and many other games could be dealt which are IMPOSSIBLE to solve within the rules.
So, this suggests two possibilities:
1. Microsoft people deliberately slipped in an IMPOSSIBLE game to cause some controversy, in which case they have certainly succeeded, or
2. Microsoft people accidentaly included an IMPOSSIBLE game.
My guess (and it’s only that) is they did it deliberately! I think it’s a little like the “Easter Egg” extras they used to hide in the good old days.
However, if you do find a solution to 11982, within the rules, you win $1,500.
Charles
If it were solvable, a computer could would be able to solve it in rather short order. I’ve built programs for such purposes and all configurations considered would be accomplished by a computer in just a few minutes.
Solving the game of Freecell (Not winning a setup, but literally SOLVING it such that you can win all winnable setups) is actually rather easy, especially compared to other complex games such as Chess. The only reason people treat it like it’s an unsolvable problem is because of the random starting positions. Because the rules are set in stone at all given times and because there are few rules to begin with, it’s easy to account for every single possible move from any point.
* You can move any card to any stack if the colors oppose and you’re placing in sequence.
* You can move any card to any empty free cell.
* You can move any card to any end cell if the suits match and you’re placing in sequence, or if it’s empty and you’re placing an ace.
These are the only rules. How much error could there possibly be in exhaustive searching? Game 11982 is… Ya know what? I’m gonna try it. I’m gonna fail and be sad, but I’m gonna try it. At least it’s a good exercise for coding.
“Game 11982 is… Ya know what? I’m gonna try it. I’m gonna fail and be sad, but I’m gonna try it.”
Well written JOSLAN!
But just think – suppose you did find a solution!
There’s $1,500 at stake.
Charles
PS – I won’t mention how long I spent on 11982 . . .
I found deal #384243 to be IMPOSSIBLE with 2 freecells!!! Can someone please prove deals 24795893 and 53687601 to be impossible and say every possible position like Adrian Wood did with 11982? I suspect 53687601 may be solvable!
And possibly 24795893.
Hi, Alex LAtham, and all.
The most interesting to find the most hard (to solve for human) – winnable deals. The most decisive
factor is the minimum length (in moves), for solutions. The most difficult deal of first million,
turned out for me, [b]255317[/b]. And this deal for solve, have a have many moves, almost longest,
from the first million, (approximately 51-53 moves).
However, in the set, more than 1 million, exists deals, with an even longer decision in 61-66 moves
and even more were found. These are all the deals I decided, but they turned out to be much harder
than the 255317 deal.
These are the most hard and most long deals, which I was able to solve –
[b] 94717719, 24515390, 9559005, 9189909. [/b]
http://freecellproject.com/?game=9189909
If you know of other deals, with very long decisions (more than 60 moves with supermoves for
solution), write please, I will be very grateful.
Thanks,
Best Regards,
Sergey.
I don’t want to play any more!
I’ve been playing Freecell since the 90s and I’ve never yet found a game I couldn’t win, however, I have only ever played the game they supplied at random so I guess I just haven’t played 11982 yet!
I got so bored with how easy the game is that I started just pressing F2 until I got 3 Aces in a line and then tried to set-up the cards with only 1 ace up and preferably no 2 and then on the last click watch the whole game play out the last 50 or 51 cards.
I guess I’ll have a go at 11982, sounds like finally there is a freecell game I won’t be able to win!
As an aside, the 4 suit spider solitaire, I haven’t yet found one of them I can’t win, might have to rewind a bit sometimes but they always seem to come out in the end.
I browse through Freecell posts from time to time. At times, I loathe coming here because of the tag “How to beat the impossible free cell game.” Of course that is click bait because there is no solution posted here.
Many years ago, in the original game in windows, when there were 12000+ games, I played them all. Every single one of them – from start to finish. I tried game 11982 several times without success, and then came back. I worked on it for a bit over two and a half months before finishing it.
Surely you would want to know the steps but I do not have them. I did not keep records of the steps for each game. But I do know that it can be done.
I do play Freecell from time to time. I have never gone on to try the new levels beyond what pops up randomly. And I have gone back to 11982 a few times to look, but never to solve; I am too old to waste another two months on that.
Have fun. But I hope that no one ever posts the actual solution; that would ruin the mystery.
6632365 cannnot win, any ideas or not winable
It is solvable. It took nearly four hours spread over a week or so and I didn’t have the screen recorder on but its not like 11982 there is at least one solution. I think I started on one of the middle columns but cant be sure. I didn’t want to spoil my 100% stat so kept trying. So take heart there is a solution.
I would love to verify your solution and gladly pay you the $1,000 reward. Get in touch!
Sorry Dan but I haven’t solved 11982 only the relatively easy one referred to in the post above namely 6632365 from bob
I have won 104,083 games in row except 11982 and still going.
>> These are the most hard and most long deals, which I was able to solve – 94717719, 24515390, 9559005, 9189909.
>> I have won 104,083 games in row except 11982 and still going.
>> I’ve been playing Freecell since the 90s and I’ve never yet found a game I couldn’t win,
Please try to solve –
93877578 ,
475577734 ,
1129622823 .
I have not solved, but I read, that someone wrote, that these numbers – WINNABLE.
Perhaps, most hard deals.
https://freecellproject.com/?game=93877578
https://freecellproject.com/?game=475577734
https://freecellproject.com/?game=1129622823
can anyone solve free cell # 6528418?
please send answer if solvable.
How about # 8381178, is it solvable?
I thought I won game 11,982 once. I have a few screenshots to prove it–no cheats. I play the iPhone app version by MobilityWare. However, MobilityWare never showed that the game had been won and never included my solution in their “show me how to win” part of the game. I wrote to them and they never gave me a satisfactory response. Finally, I went back to play the game again and record it this time, since it had not actually been very hard to beat. But the card layout for game #11,982 had changed and was now different from the one I had won. I was able to confirm this by comparing the new layout with some screenshots I had taken when I realized in the middle of playing the game that I was going to win. A little online research of Free Cell expert sights revealed that the deal I had originally played and won was not the correct deal for #11,982. I can only surmise that MobilityWare had originally misnumbered the game and corrected it since I had “played and won”, or that there is a glitch in their software that misnumbered the game for me only one time. I cannot confirm this because, again, MobilityWare has never given me a satisfactory response to my queries. So if you were playing the iPhone app MobilityWare version of FreeCell at some point in the past and thought you won game #11,982, you very well may have. It’s just that it wasn’t the real game #11,982.
I tried to include some screenshots in this post, but I can’t figure out how to do it. If there is a way, I’d appreciate it if someone would please let me know.
@Zodess Thanks for the clarification. It’s an excellent reminder for anyone claiming they’ve beat 11,982. Make sure it matches the card layout in this post.
Post 179 asked about game 8381178, we are also having problems solving it. Does anyone have any suggestions?
After 46,000+ random wins in a row (not including the streak from my last machine), I hit the wall on #11982. Ugghhhh.